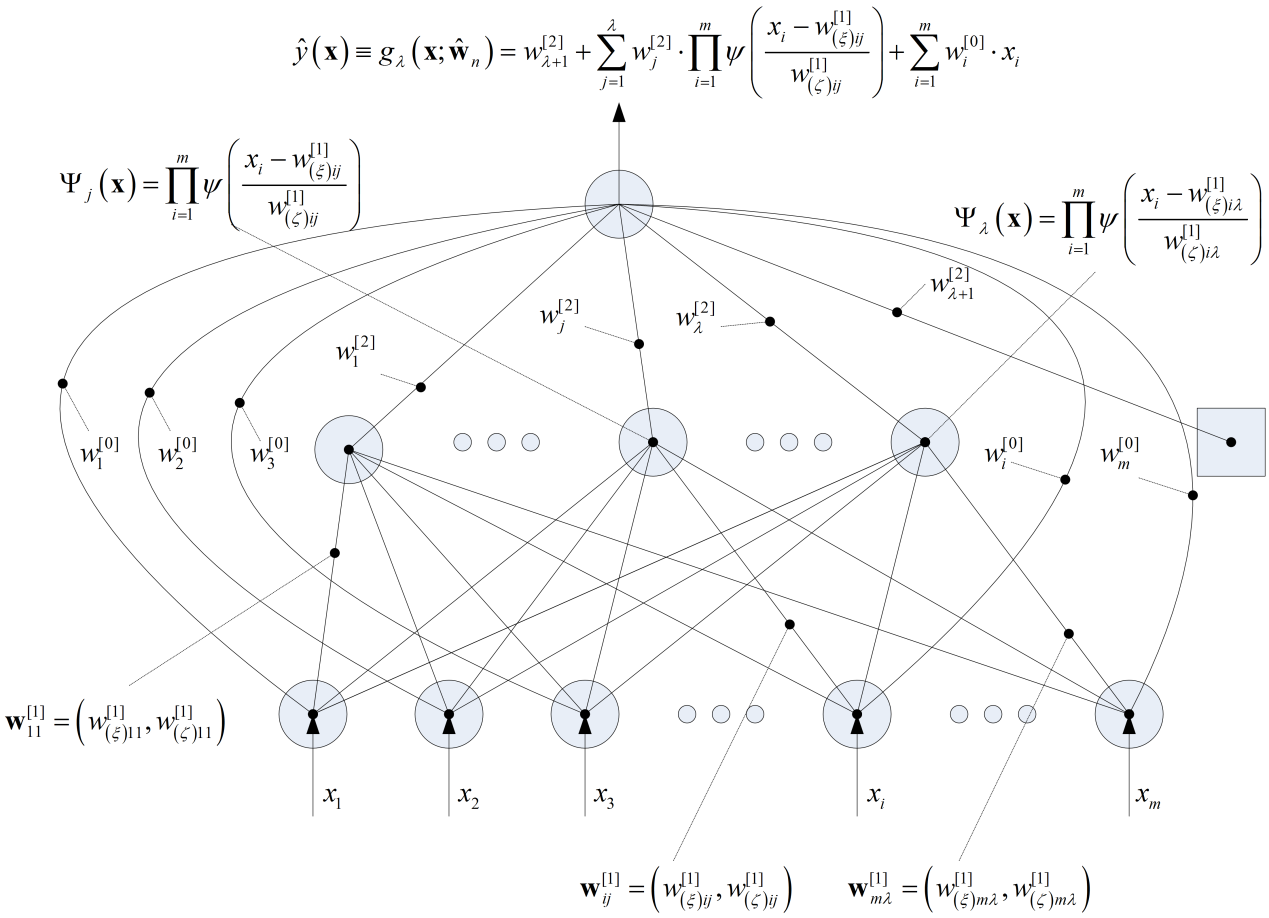
The purpose of this study is to develop a model that describes the dynamics of the daily average temperature accurately in the context of weather derivatives pricing. More precisely, we compare two state-of-the-art machine learning algorithms, namely wavelet networks and genetic programming, with the classic linear approaches that are used widely in the pricing of temperature derivatives in the financial weather market, as well as with various machine learning benchmark models such as neural networks, radial basis functions and support vector regression. The accuracy of the valuation process depends on the accuracy of the temperature forecasts. Our proposed models are evaluated and compared, both in-sample and out-of-sample, in various locations where weather derivatives are traded. Furthermore, we expand our analysis by examining the stability of the forecasting models relative to the forecasting horizon. Our findings suggest that the proposed nonlinear methods outperform the alternative linear models significantly, with wavelet networks ranking first, and that they can be used for accurate weather derivative pricing in the weather market.
Recently, a new class of financial instruments, known as “weather derivatives” has been introduced. Weather derivatives are financial instruments that can be used by organizations or individuals as part of a risk management strategy to reduce risk associated with adverse or unexpected weather conditions, (Alexandridis and Zapranis, 2013a). Just as traditional contingent claims, whose payoffs depend upon the price of some fundamental, a weather derivative has an underlying measure such as: rainfall, temperature, humidity, or snowfall. The difference from other derivatives is that the underlying asset has no value and it cannot be stored or traded while at the same time the weather should be quantified in order to be introduced in the weather derivative. To do so, temperature, rainfall, precipitation, or snowfall indices are introduced as underlying assets. However, in the majority of the weather derivatives, the underlying asset is a temperature index. Hence, in this study we focus only on temperature derivatives.
For this study DATs for several cities from around the world were selected. We used cities from 4 continents: Europe, America, Asia, and Australia. These cities were: Amsterdam, Berlin, Paris, Atlanta, Chicago, New York, Osaka, Tokyo and Melbourne. Temperature derivatives are actively traded in these cities through the CME. The data for the European cities were provided by the ECAD6 while data from the remaining cities were obtained from Bloomberg. Since we are studying 9 cities (Atlanta, New York, Chicago, Melbourne, Tokyo, Osaka, Amsterdam, Berlin, Paris) and 2 indices (HDD, CAT) for 5 dierent time periods (1, 2, 3, 6, 12 months) using two forecasting schemes (1-day-ahead, out-of-sample), the seven models (Alaton, Benth, GP, WN, NN, RBF, SVR) are compared across 180 dierent datasets.
Both in-sample and out-of-sample comparison were performed. In-sample the comparison was based on the distributional statistics of the residuals. An understanding of the dynamics that govern the residuals would provide additional information of the validity of the proposed models. We found that only in the case of the WN the initial assumption of normality was accepted in most cases. In addition, strong autocorrelation was found in the residuals of the two linear models. As a result, only the residuals of the WN satisfy the initial assumptions. This is a very important limitation of the alternative methods since they can lead to forecasts that do not represent the real evolution of the temperature dynamics leading to biased forecasts and to significant mispricing of weather derivatives.
In the out-of-sample comparison we tested our models using two forecasting schemes, namely 1-day ahead forecasting and out-of-sample forecasting. In both cases the WN outperformed all other methods, followed by Alaton, Benth and GP. The above results were also confirmed by a non-parametric Friedman test, with the Hommel’s post-hoc test. The test revealed that the WN was ranked first, Alaton second, Benth third, GP fourth, followed by NN, RBF, and SVR. It is worth mentioning that the dierence between Benth’s and GP’s ranking was not statistically significant, while GP statistically outperformed two machine learning state-of-the-art algorithms (NN and SVR).
| Table 1. Statistical test results according to the non-parametric Friedman test with the Hommel’s post-hoc test. | ||
| Algorithm | Average Rank | Adjusted PHommel |
| WN (c) | 2.1722 | – |
| Alaton | 3.0055 | 0.00012 |
| Benth | 4.3194 | 1.81E-16 |
| GPB | 4.8472 | 1.12E-24 |
| GPA | 4.8944 | 2.18E-25 |
| RBF | 5.4777 | 7.95E-37 |
| NN | 5.5444 | 3.31E-38 |
| SVR | 5.7388 | 1.47E-42 |
Finally, we examined the stability of each forecasting method relatively to the forecasting horizon. Our results indicate that the WN outperforms alternative methods in the sense that the forecasting error is more stable. The error patterns are similar for the remaining algorithms, although the changes in the error from period to period are more abrupt and often large spikes are observed.
The previous analysis indicates that our results are very promising. Modelling the DAT using the proposed method (WNs) enhanced the predictive accuracy of the temperature process. WNs can model the dynamics of the temperature very well and they can constitute an accurate method for temperature derivatives pricing. The additional accuracy of the proposed model will have an impact on the accurate pricing of temperature derivatives. In addition, the GP outperformed state-of-the-art machine learning regression algorithms, as well as Benth’s model in the out-of-sample forecasting method, indicating the usefulness of GP for pricing weather contracts before the temperature measuring period.
There is a lot of future work that can take place for the WN and GP algorithms. At the moment, the GP fitness function is a simple MSE function, and is not tailored to the problem of weather derivatives. We believe it would be beneficial to look into other fitness functions, which will take into account the HDD and CAT indices. Furthermore, another potential extension in the fitness function would be to built-in information about the pricing of weather derivatives, thus oering a generalized framework that can be applied to pricing of temperature weather derivatives.
In addition, instead of using a parametric equation for the seasonal mean, WNs can be used in order to approximate it nonlinearly and non-parametrically. We expect this method to provide a better fit to the data and to reveal the true dynamics of the evolution of the seasonal mean of the temperature. Furthermore, motivated by our promising results, in the future it is worth to examine the performance of more advance machine learning techniques such as Deep Networks and Self Organising Fuzzy Neural Networks.
This paper has been published in International Journal of Forecasting and it is a collaborative work of Dr. Antonios K. Alexandridis, Dr. Michael Kampouridis and Mr. Sam Cramer from the University of Kent.