In an earlier post I suggested that systems medicine, a new approach to medicine which applies the ‘big data’ approach of bioinformatics, offers substantial promise, but also faces profound challenges, not least the question as to how integrate multifarious sources of evidence in order to discover new causal relationships.

Here I’d like to suggest that objective Bayesian methods can offer some scope for evidence integration in systems medicine.

Objective Bayesian Epistemology (OBE) is a theory about strength of belief. It says that one’s degrees of belief should satisfy three norms:

• Probability. Degrees of belief should be probabilities.
• Calibration. Degrees of belief should fit evidence. E.g., degrees of belief should be calibrated to physical probabilities where available.
• Equivocation. Degrees of belief should otherwise equivocate between basic possibilities.

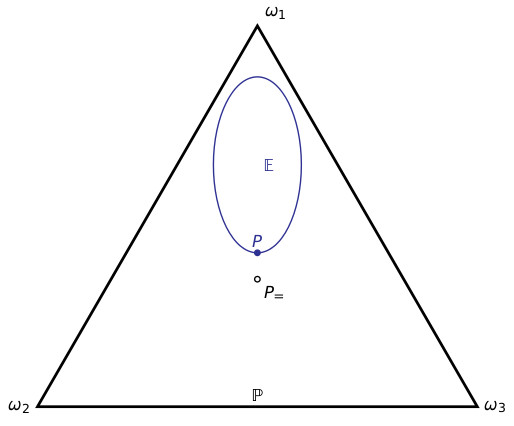
For example, suppose there are three basic (mutually exclusive and exhaustive) possibilities $latex \omega_1,\omega_2,\omega_3$. The Probability norm says that one’s degrees of belief in these three possibilities should sum to 1. I.e., one’s belief function $latex P$ should lie in the triangle depicted below. Suppose that one has a dataset; the Calibration norm says that one’s belief function should lie in the set of probability functions that match the distribution of that dataset – the region $latex \mathbb E$ below. Finally, the Equivocation norm says that one’s belief function should otherwise be as close as possible to the probability function $latex P_=$ that equivocates between the basic outcomes, i.e., which gives each basic outcome the same probability:

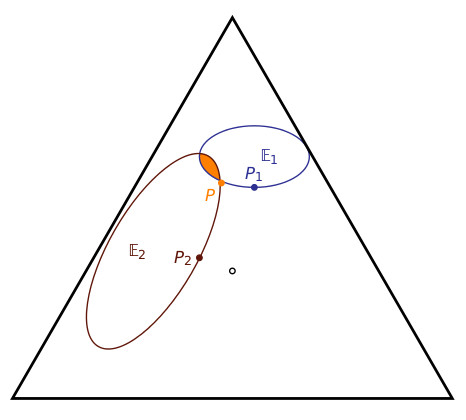
When there are two consistent datasets, the Calibration norm says that one’s belief function $latex P$ should lie in their intersection:

The OBE approach already suggests a departure from the standard practice of systems medicine. The standard approach is, for each dataset, to generate a model, called a fingerprint, which fits that dataset, and then to generate an overall model – the handprint – from those fingerprint models. (For an example of the standard approach, see point 5 on p.11 here.) In the above figure, $latex P_1$ and $latex P_2$ are the fingerprint models, and the suggestion would be to generate a handprint model which somehow aggregates the fingerprints. But the above diagram suggests something quite different: $latex P_1$ and $latex P_2$ do not provide enough information to determine the handprint model $latex P$ – one needs to determine this model directly from the datasets by focusing on the intersection of the two regions $latex \mathbb E_1, \mathbb E_2$.

The OBE approach offers further scope for evidence integration. For instance, objective Bayesian nets can be used as more efficient representations of the probability models. Recursive Bayesian nets might be employed to integrate evidence of mechanistic and causal structure into these models.

I talked about this a bit more at the recent EBM+ workshop. Slides and audio are available here.